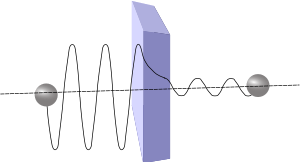
UDARNA SNAGA ISTINE - Tunel efekat

Tunel efekat ili tunelovanje je pojava u kojoj atomska čestica može da savlada konačnu potencijalnu barijeru čak i kada je njena energija niža od visine (energije) barijere. Prema klasičnoj fizici, to bi bilo nemoguće, međutim, prema zakonima kvantne mehanike, to je moguće. Na primer, alfa-raspad se objašnjava preko tunel efekta kao prodiranje alfa čestice kroz potencijalnu barijeru nuklearnih sila. Tunel efekat je našao tehničku primenu u skanirajućem tunelskom mikroskopu.

Otkriće

Tunel efekat je prvi eksperimentalno opazio Robert Vilijams Vud 1897. godine posmatrajući kretanje elektrona u emisionom polju ali nije uspeo da ga protumači. Istraživači u oblasti radioktivnog raspada još 1899. godine izražavali su nejasne sumnje o mogućnosti da do raspada dolazi zbog tunel efekta što je teorijski opisao tek Džordž Gamov, 1929. godine, nakon prethodnih otkrića Raderforda i saradnika da je alfa čestica zapravo jezgro helijuma. Mada se otkriće tunel efekta pripisuje Gamovu (koji ga je tako i imenovao) prvi teorijski opis dao je 1926/27 Fridrih Hund za opisivanje izomerije kod molekula.

Pojava i primene

Nuklearna fuzija na suncu

Pritisak i temperatura unutar sunca nisu dovoljni da obezbede da atomska jezgra mogu da savladaju Kulonovu barijeru da bi došlo nuklearne fuzije. Međutim, kvantna mehanika dozvoljava da se kulonova barijera savlada tunel efektom, sa malom, ali konačnom verovatnoćom ^[1]

Biološka evolucija

Nestabilnost genetskog koda je, između ostalog, uzrokovana konačnom verovatnoćom za tunelovanje protona u DNK. Dakle, tunel efekat je delimično odgovoran za nastanak spontanih mutacija. ^[2].

Alfa-raspad

Na tunel efektu počiva, između ostalog, spontani radioaktivni alfa-raspad, na primer, jezgra uranijuma. Prema klasičnoj fizici jezgro uranijuma ne bi trebalo da se raspada, jer je energijska barijera jake interakcije previsoka. Međutim, zbog tunel efekta postoji vrlo mala, ali konačna, verovatnoća da se alfa čestica nađe s druge strane barijere, dakle, van domašaja nuklearnih sila. U odsustvu nuklearnih sila, kulonova odbojna sila (pozitivno jezgro odbija pozitivnu alfa česticu) postaje dominantna te alfa čestica ogromnom brzinom napušta okolinu jezgra-roditelja.

Kratak kvantno-mehanički opis

Prema klasičnoj mehanici, čestica može u prostoru može da se nađe samo tamo gde je njena potencijalna energija manja od ukupne. Ovo sledi iz činjenice da kinetička energija čestice

~{E_{\rm {kin}}}={\frac {p^{2}}{2m}}={E}-{U_{\rm {pot}}}

ne može (po klasičnoj fizici) biti negativna, jer bi tada impuls bio imaginarna veličina.

Dakle, ako se dva regiona prostora razdvoje potencijalnom barijerom, tako da

~{U_{\rm {pot}}}>{E}

, prolaz čestice kroz barijeru u klasičnoj teoriji je nemoguć. Što se zaista eksperimentalno opaža za makroskopska tela - niko nije prošao kroz zatvorena vrata. U kvantnoj mehanici, imaginarna vrednost impulsa označava samo da umesto konstantnog talasa talasna funkcija prelazi u eksponencijalnu, dakle monotonu, zavisnost od koordinata. To je očigledno iz Šredingerove jednačine sa stalnim potencijalom (radi jednostavnosti uzimamo jednodimenzionalni slučaj):

~{\frac {{{\rm {d}}^{2}}{\psi }}{{{\rm {d}}{x}}^{2}}}+{\frac {2m}{{\hbar }^{2}}}{\left({E}-{U_{\rm {pot}}}\right)}{\psi }=0

~{\psi }=A\exp {\left(ix{\frac {\sqrt {2m{\left({E}-{U_{\rm {pot}}}\right)}}}{\hbar }}\right)}+B\exp {\left(-ix{\frac {\sqrt {2m{\left({E}-{U_{\rm {pot}}}\right)}}}{\hbar }}\right)}

Neka se na putu čestice nađe barijera potencijala (visine)

~U_{0}

, i neka je potencijal čestice pre i posle prolaska kroz barijeru jednak nuli.

Za regione

~I

(pre prolaza),

~II

(u prolazu unutar barijere), i

~III

(nakon prolaska kroz barijeru) (početak barijere poklapa se sa koordinatnim početkom a njena „širina“ je

~a

), dobijamo svojstvenu funkciju

~{{\psi }_{II}}={A_{2}}\exp {\left(-{\chi }x\right)}+{B_{2}}\exp {\left({\chi }x\right)}

~{{\psi }_{III}}={A_{3}}\exp {\left(ik(x-a)\right)}+{B_{3}}\exp {\left(-ik(x-a)\right)}

Pošto član

~{B_{3}}\exp {\left(-ik(x-a)\right)}

opisuje odbijeni talas koji se kreće iz beskonačnosti, a koji u posmatranom slučaju ne postoji, sledi da je

~{B_{3}}=0

. Da bi opisali veličinu tunel efekta, uvedimo koeficijent propusnosti barijere jednak modulu odnosa gustine toka čestica koje su prošle kroz barijeru i gustine toka upadnih čestica:

~D={\frac {{\mathcal {j}}{j_{III}}{\mathcal {j}}}{{\mathcal {j}}{j_{I}}{\mathcal {j}}}}

~{j}={\frac {i{\hbar }e}{2m}}{\left({\frac {{\partial }{{\psi }^{*}}}{{\partial }x}}{\psi }-{\frac {{\partial }{\psi }}{{\partial }x}}{{\psi }^{*}}\right)}

~{D}={\frac {{{\mathcal {j}}{A_{3}}{\mathcal {j}}}^{2}}{{{\mathcal {j}}{A_{1}}{\mathcal {j}}}^{2}}}

Kristeći granične uslove prvo izrazimo

~A_{2}

~B_{2}

preko

~A_{3}

(s tim što je

~{\chi }a~{\gg }~1

~{A_{2}}={\frac {1-in}{2}}{A_{3}}{\exp {\left({\chi }a\right)}}~,~~~~~~{B_{2}}={\frac {1+in}{2}}{A_{3}}{\exp {\left(-{\chi }a\right)}}~{\approx }~0

~{A_{1}}={\frac {{\left(1-in\right)}{\left(1+{\frac {i}{n}}\right)}}{4}}{\exp {\left({\chi }a\right)}}{A_{3}}

~D~{\cong }~{D_{0}}{\exp {\left(-{\frac {2a{\sqrt {2m{\left({U_{0}}-E\right)}}}}{\hbar }}\right)}}

~{\frac {2a{\sqrt {2m{\left({U_{0}}-E\right)}}}}{\hbar }}~{\Rrightarrow }~{\frac {2}{\hbar }}{\int \limits _{x_{1}}^{x_{2}}{\sqrt {2m{\left({U(x)}-E\right)}}}\,{\rm {d}}x}

~D~{\cong }~{D_{0}}{\exp {\left(-{\frac {2}{\hbar }}{\int \limits _{x_{1}}^{x_{2}}{\sqrt {2m{\left({U(x)}-E\right)}}}\,{\rm {d}}x}\right)}}

Dakle, i kada je potencijalna energija barijere veća od ukupne energije čestice verovatnoća za prolazak čestice kroz barijeru je konačna (mada najčešće samo malko veća od nule). Veličina verovatnoće (izražena preko koeficijenta propusnosti) zavisi od mase čestice, debljine brijere i relativnog odnosa energija barijere i čestice. Pošto se masa čestice kod koeficijenta propusnosti javlja u eksponentu, verovatnoća za tunel efekat kod masivnih čestica opada ogromnom brzinom te se efekat praktično javlja samo kod mikroskopskih objekata.

Reference

Wolschin, G.: Thermonuclear Processes in Stars and Stellar Neutrinos, in: Castell, L.; Ischebeck, O. (Eds.): Time, Quantum and Information, Part II, pp. 115-134. Springer-Verlag, Berlin, Heidelberg, New York 2003.

Löwdin, P.-O.: Proton Tunneling in DNA and its Biological Implications. Reviews of Modern Physics 35 (3), 724-732 (1963).

Literatura

Robert Williams Wood: A new form of Cathode Discharge and the Production of X-Rays, together with some Notes on Diffraction, Phys. Rev. 5, 1 (1897)
George Gamow: Zur Quantentheorie des Atomkernes, Z. Phys. 51, 204 (1928)
Ronald W. Gurney und Edward U. Condon: Wave Mechanics and Radioactive Disintegration, Nature 122, 439 (1928)
R. Holm: The Electric Tunnel Effect across Thin Insulator Films in Contact, J. Appl. Phys. 22, 569 (1951)
J. C. Fisher und Ivar Giaever: Tunneling Through Thin Insulating Layers, J. Appl. Phys. 32, 172 (1961)
Brian D. Josephson: Possible New Effects in Superconducting Tunneling, Phys. Lett. 1, 251 (1962)
Philip W. Anderson, J. M. Rowell und D. E. Thomas: Image of the Phonon Spectroscopy in the Tunneling Characteristic between Superconductors, Phys. Rev. Lett. 10, 334 (1963)
Sidney Shapiro: Josephson Current in Superconducting Tunneling: The Effect of Microwaves and other Observations, Phys. Rev. Lett. 11, 80 (1963)
Gerd Binnig, Heinrich Rohrer, C. Gerber und E. Weibel: Tunneling through a Controllable Vacuum Gap, Appl. Phys. Lett. 40, 178 (1982)
Dilip K.Roy: Quantum mechanical tunnelling and its applications. World Scientific, Singapore. 1986. ISBN 9971-5-0024-8
Shin Takagi: Macroscopic quantum tunneling. Cambridge Univ. Press, Cambridge. 2002. ISBN 0-521-80002-1
Joachim Ankerhold: Quantum tunneling in complex systems - the semiclassical approach. Springer, Berlin 2007. ISBN 978-3-540-68074-1.
S. Macura, J. Radić-Perić, ATOMISTIKA, Fakultet za fizičku hemiju Univerziteta u Beogradu/Službeni list, Beograd, 2004., str. 516.

Tunel efekat

Sadržaj